Teori Dasar Graf
Teori Graf mulai dikenal pada saat seseorang matematikawan bansa Swiss, bernama Leonhard Euler, berhasil mengungkapkan Misteri jembatan Konigsberg pada tahun 1736, berhasil mengungkapkan misteri jembatan Konigsberg pada tahun 1736.
Di Kota Konigsberg (sekarang bernama Klilingrad, di Uni Soviet) mengalir sebuah sungai bernama sungai Pregel. Di tengah sungan tersebut terdapat dua buah pulau. Dari kedua pulau tersebut terdapat jembatan yang menghubung ke tepian sungai dan diantara kedua pulau. Jumlah jembatan tersebut adalah 7 buah seperti gambar berikut :
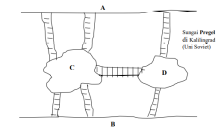
- Euler, menyajikan keadaan jembatan Konigsberg tersebut seperti gambar, berikut :
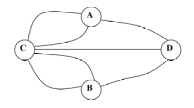
- Daratan (Tepian A dan B, serta pulau C dan D) disajikan sebagai titik.
- Jembatan disajikan sebagai ruas garis.
Euler mengemukakan teoramanya yang mengatakan bahwa pejalanan yang diiginkan diatas (yang kemundian dikenal sebagai perjalanan Euler) akan ada apabila graf terhubung dan banyaknya garis yang datang tidak pada setiap titik derajat simpul adalah genap.
Graf secara Formal
Sebuah Graf G mengandung 2 himpunan :
(1) Himp V, yang elemennya tersebut simpul
Vertex / point / titik / node
(2) Himp E, yang merupakan pasangan tak terurut dari simpul-simpul, disebut ruas
Edge/rusuk/sisi
Sehingga sebuah graf dinotasikan sebagai G (V,E)
Contoh :
G (V,E) V = {A,B,C,D} E = { (A,B), (B,C), (C,D), (D,A), (B,D)
Secara Geometri :
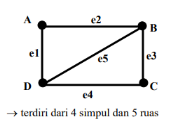
Tidak ada ketentuan khusus dalam penyajian graf secara geometri, seperti dmana dan bagaimana menyajikan simpul dan ruas. Berikut contoh penyajian Graf yang sama, tetapi disajikan berbeda.
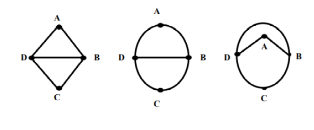
Beberapa istilah lain dalam graf :
- Berdampingan simpul U dan V disebut berdampingan bila terdapat ruas (U,V)
- Order banyaknya simpul
- Size banyaknya ruas
- Self-loop(loop) / Gelung ruas yang menghubungkan simpul yang sama (sebuah simpul)
- Ruas sejajar / berganda ruas-ruas yang menghubungkan 2 simpul yang sama.
Sebuah Graf dikatakan multigraf bila graf tersebut mengandung ruas sejajar atau gelung. Sedangkan graf yang tidak mengandung ruas sejajar atau gelung dikenal graf sederhana, atau yang disebut graf. Adapun contoh multigraf adalah sebagai berikut :
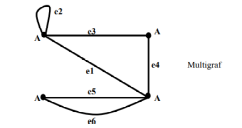
Subgraf
G’(V’,E’) adalah Subgraf dari G (V,E) bila : V’ V dan E’ E apabila E’ mengandung semua ruas di E yang kedua ujungnya di V’, maka G’ adalah Subgraf yang dibentuk oleh V (Spanning Subgraph)
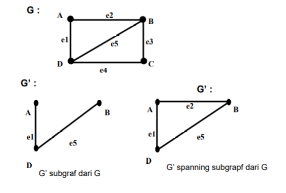
Graf Berlabel
Graf berlabel / berbobot adalah graf yang sama setiap ruasnya mempunyai nilai/bobot berupa bilangan non negatif. Contoh :
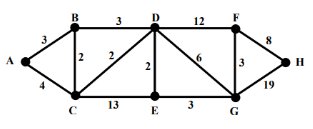
Graf Isomorfis
Dua buah graf G1 dan G2 dikatakan isomorfik jika terdapat korespondensi satu-satu antara simpul-simpul keduanya dan antara sisi-sisi keduanya sehingga jika sisi e bersisian dengan simpul u dan v pada G1 maka sisi e pada G2 juga bersisian dengan simpul u’ dan v’ (Munir, 2003)
Dua buah graf yang isomorfik adalah graf yang sama, kecuali penamaan simpul dan sisinya saja yang berbeda. Selain menunjukkan korespondensi satu-satu diantara kedua himpunan simpul graf, dua buah graf dikatakan isomorfik jika memenuhi ketiga syarat berikut.
- Mempunyai jumlah simpul yang sama.
- Mempunyai jumlah jalur yang sama
- Mempunyai jumlah simpul yang sama berderajat tertentu (Munir, 2003)
Graf Isomorfis
Graf Homomorfis
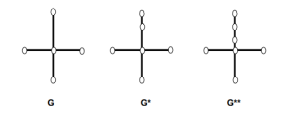
Jika G* dan G** diperoleh dari G dengan membagi beberapa ruas dari G oleh penambahan beberapa simpul pada ruas tersebut, maka kedua graf G* dan G** disebut homomorfis.
Definisi Teori Algoritma
Istilah algoritma pertama kali diperkenalkan oleh ahli matematika yaitu Abu Jaf’ar Muhammad Ibnu Musa Al Khawarizmi,
Yang dimaksud dengan algoritma adalah : Urutan dari barisan instruksi untuk menyelesaikan suatu masalah. Adapun algoritma dapat dinyatakan dalam bentuk : flow chart, diagram alur, bahasa semu
Sedangkan secara bahasa, algoritma berarti suatu metode khusus untk menyelesaikan suatu masalah yang nyata (dari Webster Dictionary)
Kriteria Algoritma
Dari suatu permasalahan yang akan diselesaikan, bisa terjadi terdapat lebih dari satu algoritma
Dalam memilih algoritma yang terbaik yang dapat digunakan, harus diperhatikan beberapa kriteria-kriteria tersebut antara lain :
- Efektif dan Efisien
- Jumlah langkahnya berhingga
- Berakhir
- Ada Output
- Terstruktur
Algoritma
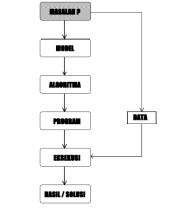
Adapun langkah-langkah yang dilakukan dalam proses penyelesaian masalah dengan bantuan komputer adalah sebagai berikut :